[latexpage]
La gravità dell’epidemia di COVID-19 (dichiarata pandemia l’11 marzo 2020) è innegabile. In correlazione, il trend delle ultime settimane sembra suggerire che ognuno, improvvisandosi analista, provi a dar vita a variazioni sul tema di un medesimo grafico, che mostra il numero cumulativo di contagi o di morti in funzione del tempo.
Estrapolazioni di numeri irrealistici, previsioni su quando un Paese possa “superarne” un altro, considerazioni sul successo o il fallimento delle misure di contenimento: questi sono alcuni dei “divertissement” che ne conseguono.
Portare ordine in un mondo caotico è da sempre l’impulso motore del progresso umano. Tuttavia, mentre ci sono solide ragioni per aspettarsi andamenti esponenziali nelle fasi iniziali della diffusione di un’epidemia, ci sono molti fattori pratici che cospirano contro l’efficacia di un semplice fit alle curve. Un po’ di conoscenza di modellizzazione epidemica può essere di grande aiuto.
Indice dell'articolo
Modelli compartimentali
La modellistica in epidemiologia ha una lunga e ricca storia, risalente già agli anni ’20 del Novecento. L’idea alla base è ingannevolmente semplice: possiamo dividere la popolazione in vari compartimenti, rappresentativi delle diverse fasi della malattia, e usare la dimensione relativa di ciascun compartimento per modellizzarne l’evoluzione nel tempo.
Modello SI
Cominciamo dal pi๠semplice di questi modelli: il modello susceptible-infected (SI). Dividiamo allora la popolazione in due compartimenti, quello dei sani (susceptible) e quello degli infetti. La dinamica è altrettanto semplice: quando una persona sana viene a contatto con una infetta, diventa a sua volta infetta con una data probabilità . Simbolicamente, $$S+I\overset{\beta}{\longrightarrow}I,$$ dove β rappresenta il tasso d’infezione. Perchà© questo modello non soddisfa? Perchà©, se sei infetto, lo saresti per sempre. Non sorprende che, dato sufficiente tempo, tutti diventerebbero infetti. Non molto interessante.
Modello SIR
Un modello pi๠realistico si può sviluppare aggiungendo un altro compartimento, ossia un’altra possibile transizione. L’estensione pi๠comune porta al modello susceptible-infectious-recovered (SIR). Il compartimento che abbiamo aggiunto rappresenta le persone che sono state malate e che sono guarite, divenendo immuni (assunzione forte del modello – la discuteremo meglio in relazione a COVID-19). Chiaramente, questo nuovo compartimento ora riduce lentamente il numero di infetti, i quali possono cioè guarire col passare del tempo. In termini di transizioni, ciò si traduce in $$\begin{array}{ccc}
S+I & \overset{\beta}{\longrightarrow} & I\
\\ I & \overset{\mu}{\longrightarrow} & R
\end{array},$$ dove μ è il tasso di transizione spontanea da infetto a guarito. Non è difficile intuire che, a un dato momento, il numero di guariti dipende solo dal numero di infetti a quel momento.
Se risolviamo matematicamente le equazioni del modello SIR, troviamo grafici del tipo:
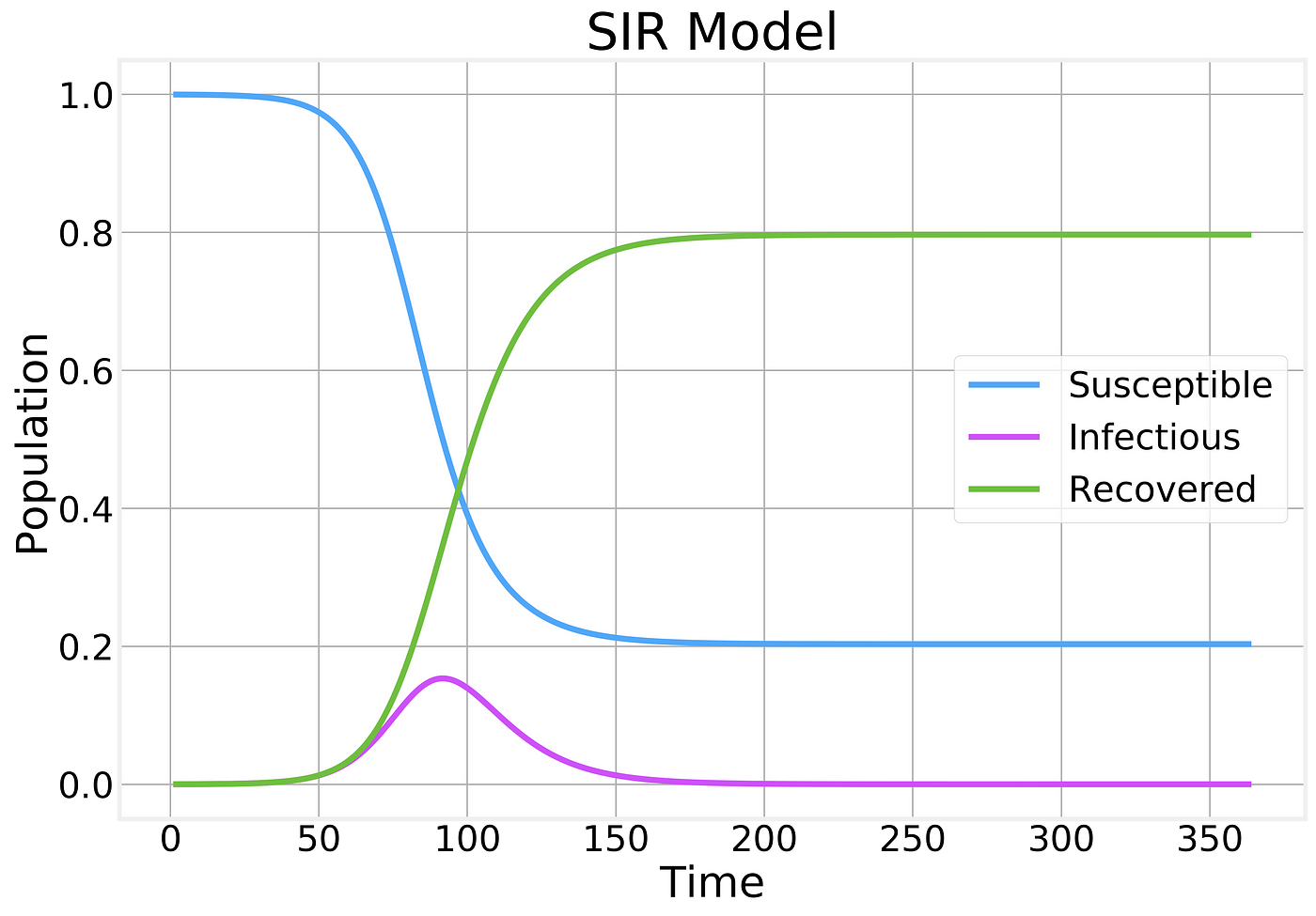
Facciamo alcune osservazioni:
- il numero di suscettibili può solo decrescere;
- il numero di guariti può solo crescere;
- e il numero di infetti cresce fino a un certo punto, quando raggiunge un picco da cui comincia a decrescere;
- una parte significativa della popolazione diventa infetta e, alla fine, guarisce;
- c’è un’ovvia limitazione intrinseca al modello siffatto, perchà© non stiamo prevedendo un esito spiacevole, ma possibile: la morte.
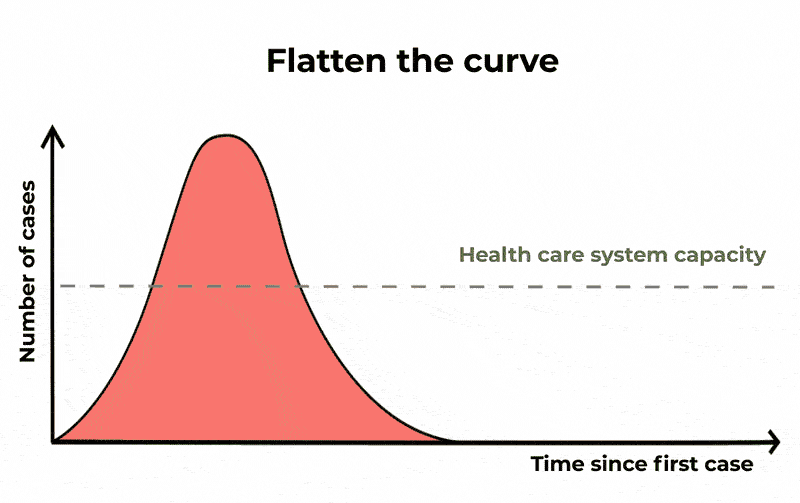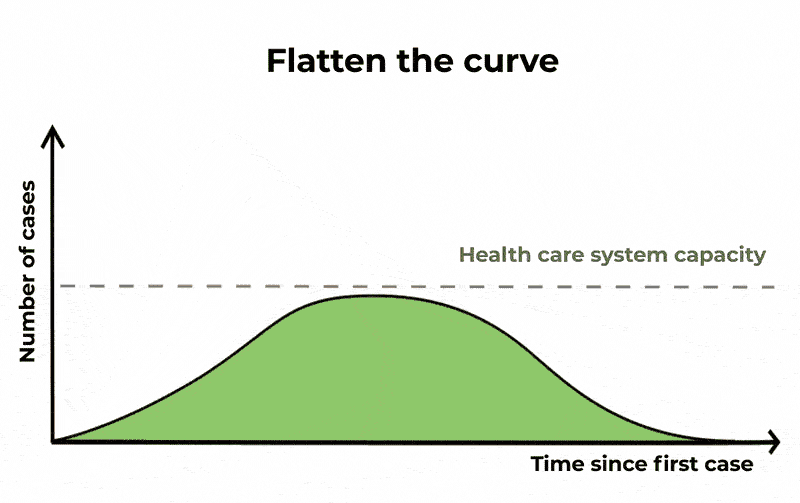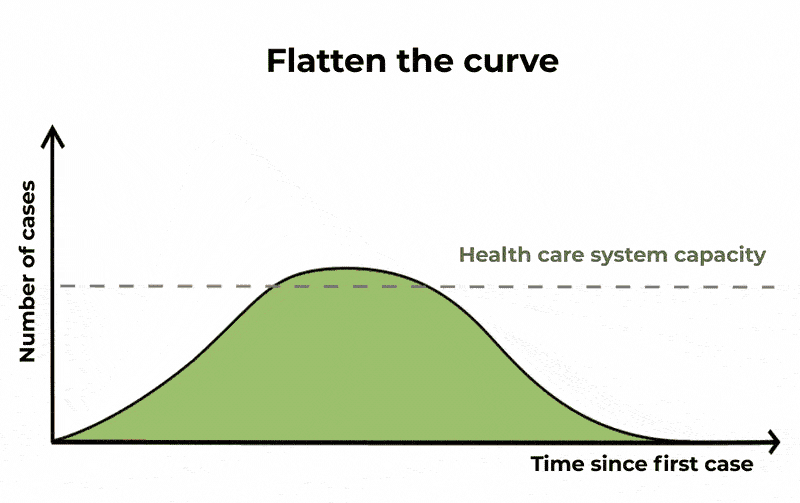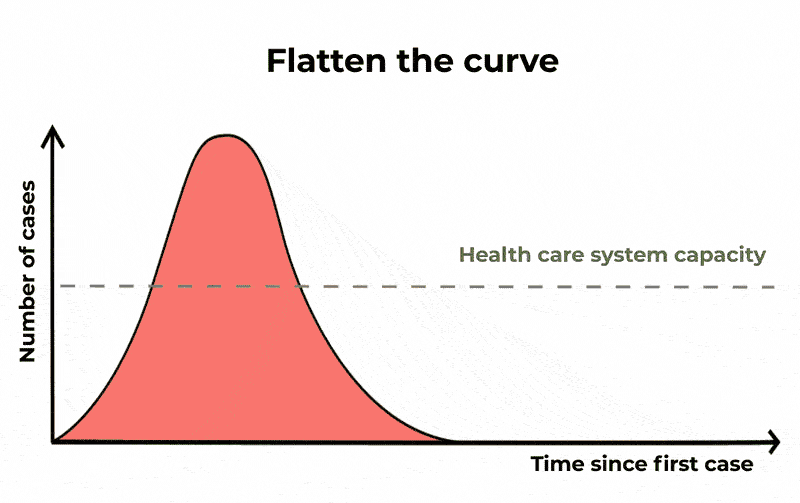
Come osservato, guardando al solo compartimento degli infetti, scopriamo che una frazione significativa della popolazione può risultare infetta allo stesso momento. Questa sarebbe una potenziale causa di sovraccarico per il sistema sanitario – la cui gravità dipende dalla severità dell’infezione. Quando sentiamo parlare di appiattimento della curva, è questo ciò a cui ci si riferisce.
Andamento esponenziale dell’epidemia
Dall’espressione matematica del modello SIR, si possono ottenere alcuni risultati semplici, ma interessanti. In particolare, se ci concentriamo sulle primissime fasi dello spread epidemico, possiamo assumere che la frazione di suscettibili si identifichi quasi perfettamente con l’intera popolazione. Troveremmo $$I\left(t\right)\simeq I_{0}e^{\mu\left(R_{0}-1\right)t},$$ovvero l’esponenziale che tutti cercano di utilizzare per comprendere l’andamento dell’epidemia. Notiamo la presenza del parametro $$R_{0}\equiv\frac{\beta}{\mu},$$chiamato tasso netto di riproduzione della malattia (Râ‚’). Questo fattore è ciò che definisce se ci sarà o meno un’epidemia: se è minore di 1, la malattia si estingue; altrimenti, si espande in maniera tragicamente esponenziale.
Una maniera intuitiva di interpretare Râ‚’ è come numero medio di nuove infezioni prodotte da un singolo individuo infetto. Se una persona infetta, prima di guarire, è capace di diffondere la malattia ad almeno un’altra persona, allora l’epidemia continua; in caso contrario, l’epidemia si estingue. Questo parametro è dunque quel che occorre determinare, e dipende da molti fattori diversi che sono caratteristici del virus.
Alla data di stesura di questo articolo, le migliori stime di Râ‚’ per SARS-CoV-2, il coronavirus che causa COVID-19, si attestano intorno a 2.5.
Râ‚’, destino dell’epidemia e immunità di gregge
Guardando all’equazione che regge l’evoluzione nel tempo della frazione di infetti, scopriamo un cambio nel suo andamento quando si verifica la condizione (che definisce il tasso efficace di riproduzione)$$R_{{\rm eff}}\left(t\right)\equiv R_{0}\frac{S\left(t\right)}{N}<1,$$essendo la dimensione totale della popolazione data da$$N\equiv S\left(t\right)+I\left(t\right)+R\left(t\right),$$assunta costante nel tempo – i.e. non è prevista la morte; oppure le morti sono bilanciate dalle nascite.
Il tasso efficace di riproduzione governa il punto in cui raggiungiamo il picco epidemico, dopo il quale – se tutte le condizioni restano inalterate – l’epidemia comincia a spegnersi.
Nel contesto di un modello ancora semplice per il mondo reale, il picco rappresenta il punto in cui la popolazione comincia ad avere abbastanza di quella che è nota come immunità di gregge, che impedisce al contagio di espandersi oltre. Quando un vaccino è disponibile, i programmi di vaccinazione sono concepiti per aiutare la popolazione a raggiungere l’immunità di gregge, senza dover attendere che una sua quota significativa risulti infetta.
Râ‚’ determina pure la frazione finale della popolazione che non risulta colpita. I valori stimati per SARS-CoV-2 conducono a una percentuale di individui mai infettati che, dopo un tempo sufficiente per far seguire all’epidemia il suo corso, spazia fra il 20% e il 10%.
Verso modelli migliori
Questo era solo un assaggio degli aspetti basilari della modellistica epidemiologica. La realtà è ben pi๠complicata di cosà¬. Eppure, come detto all’inizio dell’articolo, tutti sembrano proporci delle analisi. Quanto sono attendibili? Si può raggiungere una descrizione matematica pi๠fedele alla realtà ? A breve lo approfondiremo in un altro articolo.
Vincenzo Ventriglia
Bibliografia
- Epidemic Modeling 101: Or why your CoVID19 exponential fits are wrong (https://medium.com/data-for-science/epidemic-modeling-101-or-why-your-covid19-exponential-fits-are-wrong-97aa50c55f8
- Introduction to SEIR Models, Nakul Chitnis (Swiss TPH)